Новую модификацию Creta назвали Diamond, она разработана бразильским подразделением Hyundai. Пока это лишь концепт, однако, как заявили в Hyundai, в…
Continue ReadingNissan 370Z пережил пересадку «сердца» ещё до смены поколений
Автопроизводители всё чаще сотрудничают с лучшими представителями тюнинг-индустрии, от услуг которых прежде отговаривали, пугая клиентов потерей заводской гарантии. Между тем…
Continue ReadingРайдшеринг – это не автобусы! BlaBlaCar опять пытаются запретить в России
Транспортники не первый раз атакуют сервис BlaBlaCar. Ровно год назад прокуратура Краснодарского края и Региональный автотранспортный союз (РАС) сумели доказать…
Continue ReadingVolkswagen прирастает пикапами: готовится конкурент для Fiat Toro и Renault Duster Oroch
Пока Volkswagen распространил только одно изображение пикапа, имя машины не раскрывается. Новинка представляет собой концепт, однако решение о запуске грузовика…
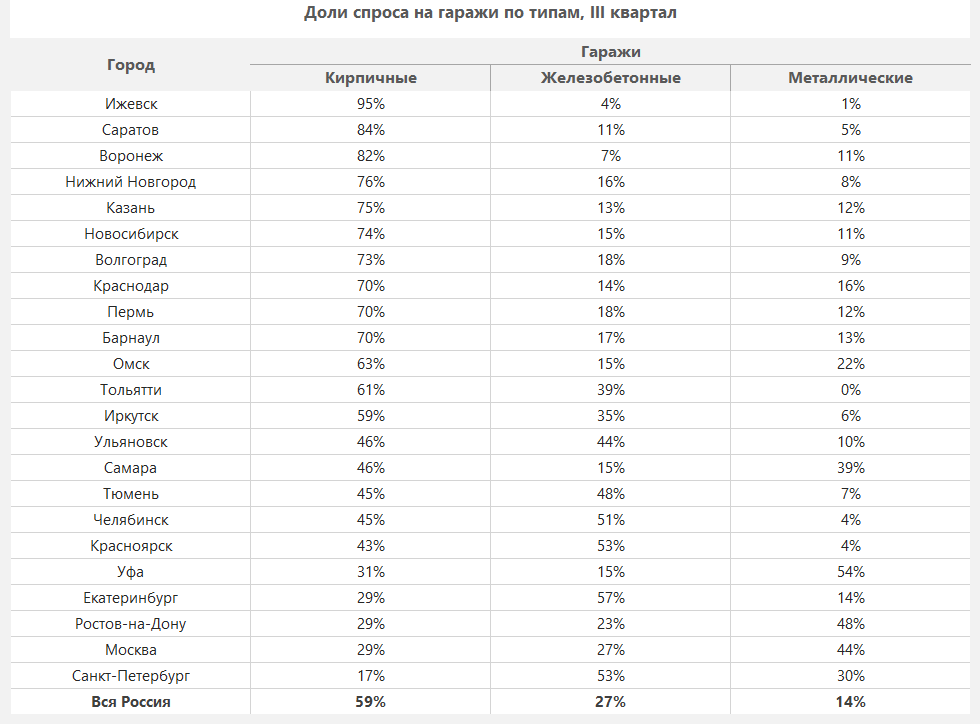
Continue ReadingАвтовладельцы не могут расстаться со своими гаражами
Распределение «внутригаражного» спроса по типам материала постройки также ожидаемо оказалось в пользу более «монолитных» конструкций из кирпича и железобетона: кирпичные…
Continue ReadingКроссовер Hyundai Saga станет примером для обновлённого семейства бюджетников
Новинку назвали Saga EV, в Hyundai ее относят к сегменту SUV. Это не серийный автомобиль, а концепт, он дебютирует на…
Continue ReadingРоссийское аэротакси Bartini уже летает, но оно пока маленькое…
Разработкой летательных аппаратов, которые в перспективе заменят автомобили, сегодня занимаются многие крупные компании (в частности, Toyota, Airbus, Uber) и сотни…
Continue ReadingПлавятся «мозги»: Audi опять отзывает автомобили в России
В июне Audi уже отзывала в России 728 машин означенных моделей из-за риска попадания влаги в электронные компоненты и, как…
Continue ReadingСменивший бренд SsangYong Rexton попробует отбить покупателей у Toyota Fortuner за счёт цены
Предсерийный внедорожник Mahindra дебютировал в феврале этого года на домашнем автосалоне, ранее машина была известна под индексом Y400. Теперь же…
Continue ReadingВ каких случаях можно вернуть дилеру бракованный автомобиль? Разъяснения Верховного суда
«Не доволен – иди в суд!» – это правило жизни, давно укоренившееся в западных странах, у нас пока только прививается,…
Continue Reading